Η κβαντομηχανική μας λέει πως τα σωματίδια μπορεί να είναι σε πολλές θέσεις ταυτόχρονα, «απλωμένα σε ένα κύμα πιθανοτήτων»
Γιατί δεν μπορούμε να πούμε απλώς ότι τα σωματίδια έχουν σαφείς, ορισμένες θέσεις, και ότι μόνο η γνώση μας δεν είναι πλήρης; Επειδή όπως δείχνει το Θεώρημα του Bell, θα μπλέξουμε σε προβλήματα!
John Stewart Bell (1928-1990), Βρετανός Φυσικός, στο CERN (το Ευρωπαϊκό εργαστήριο σωματιδιακής φυσικής). Ο Bell είναι περισσότερο διάσημος για τη διατύπωση του Θεωρήματος Μπελ στα μέσα της δεκαετίας του 1960. Το έργο του Μπελ επέκτεινε το παράδοξο EPR ώστε να εξάγει αυτό που είναι γνωστό ως η ανισότητα Μπελ. Αυτό συνεπάγεται ότι ορισμένοι τύποι φυσικών θεωριών είναι αδύνατον να ισχύουν για όλες τις προβλέψεις της κβαντομηχανικής, εγείροντας φιλοσοφικά ερωτήματα σχετικά με τα όρια του τι είναι δυνατόν με τέτοιες θεωρίες. Φωτογραφήθηκε το 1989, στο Μεγάλο Επιταχυντή Ηλεκτρονίων-Ποζιτρονίων, στο CERN της Ελβετίας.
Η διάταξη που πειραματιζόμαστε είναι μία πηγή η οποία εκπέμπει διεμπλεκόμενα ζεύγη σωματιδίων. Κάθε σωματίδιο κατευθύνεται σε έναν ξεχωριστό ανιχνευτή. Αυτά τα διεμπλεκόμενα σωματίδια παρουσιάζουν παράξενους συσχετισμούς στη συμπεριφορά τους. Αν μετρήσουμε το κάθετο σπιν του κάθε σωματιδίου, τότε και τα δύο σωματίδια (του ζεύγους) είναι εγγυημένο ότι θα δώσουν το ίδιο αποτέλεσμα. Ωστόσο, δεν είμαστε υποχρεωμένοι να μετράμε πάντα το κάθετο σπιν. Μπορούμε επίσης να μετράμε το οριζόντιο σπιν, ή οποιαδήποτε γωνία ενδιάμεσα οριζόντιου και κάθετου. Ας μείνουμε πάνω σε αυτό.
Πρόκειται να χρησιμοποιήσουμε 3 διαφορετικές ρυθμίσεις για τους δύο ανιχνευτές.
Η ρύθμιση Α θέτει το ερώτημα: «Είναι το σπιν τους προς τα πάνω;»
Η ρύθμιση Β θέτει το ερώτημα: «Είναι το σπιν τους προς τα δεξιά;»
Η ρύθμιση C θέτει το ερώτημα: «Είναι το σπιν τους προς μια γωνία 45 μοιρών μεταξύ των ‘πάνω’ και ‘δεξιά’;»
Αν και οι δύο ανιχνευτές είναι στη ρύθμιση Α, τότε και οι δύο δίνουν την ίδια απάντηση για κάθε δεδομένο διεμπλεκόμενο ζεύγος σωματιδίων. Ομοίως, θα δώσουν την ίδια απάντηση, αν και οι δύο βρίσκονται στη ρύθμιση Β, ή και οι δύο βρίσκονται στη ρύθμιση C.
Ας υποθέσουμε ότι κάθε σωματίδιο έχει προκαθορισμένες απαντήσεις σε κάθε ένα από αυτά τα 3 ερωτήματα. Εμείς απλά δεν γνωρίζουμε τις απαντήσεις ακόμα! Μπορούμε να περιγράψουμε κάθε σωματίδιο σαν ένα σύνολο από 3 απαντήσεις στα ερωτήματα που τίθενται από τους ανιχνευτές Α, Β και C. Για παράδειγμα, θα μπορούσαμε να χρησιμοποιήσουμε (Y,Y,Ν) για να υποδηλώσουμε ένα σωματίδιο το οποίο θα απαντήσει «ναι» στο Α και B, αλλά «όχι» στο C. Ομοίως, το (Y,Ν,Υ) θα υποδηλώνει ένα σωματίδιο που θα απαντήσει «όχι» στο Β, αλλά «ναι» στο Α και στο C.
Υπενθυμίζουμε ότι αν και οι δύο ανιχνευτές είναι στην ίδια ρύθμιση, τότε και τα δύο σωματίδια θα δώσουν την ίδια απάντηση. Αυτό σημαίνει ότι και τα δύο ηλεκτρόνια σε ένα ζεύγος μπορούν να περιγραφούν με το ίδιο σύνολο τριών απαντήσεων. Κάθε ζεύγος σωματιδίων μπορεί να τοποθετηθεί κάπου σε αυτό το διάγραμμα Venn:
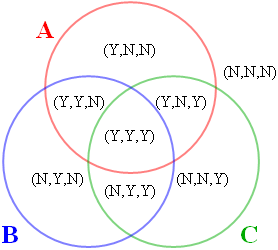Υπάρχουν οκτώ πιθανές θέσεις στο διάγραμμα Venn, αλλά δεν υπάρχει κανένας λόγος να υποθέσουμε ότι κάθε ενδεχόμενο είναι ισοπίθανο. Μήπως θα μπορούσαμε να καθορίσουμε την πιθανότητα κάθε ενδεχομένου; Αλλά είναι είναι κάπως δύσκολο. Το πρόβλημα είναι ότι μπορούμε να προσδιορίσουμε μόνο δύο από τις απαντήσεις για κάθε δεδομένο ζεύγος σωματιδίων. Μόλις μετρηθεί το σωματίδιο, έχουμε αλλάξει την αρχική κβαντική του κατάσταση και δεν μπορούμε πλέον να το διερευνήσουμε. Παρ ‘όλα αυτά, μπορούμε να γίνουμε μαθηματικοί ντετέκτιβς και να τα καταλάβουμε όλα, σωστά;
Λοιπόν, ας πούμε ότι έχουμε θέσει τον πρώτο ανιχνευτή στη ρύθμιση Α και το δεύτερο στη ρύθμιση C. Πόσο συχνά είναι η απάντηση του Α διαφορετική από την απάντηση του C; Δηλαδή, πόσο συχνά τα ζεύγη των σωματιδίων εμπίπτουν στη σκιασμένη περιοχή που φαίνεται στο σχήμα (a); Η απάντηση είναι περίπου 15% των περιπτώσεων. Αυτό μπορεί να προβλεφθεί από την κβαντική θεωρία, αλλά εξίσου σημαντικό είναι, ότι μπορεί να παρατηρηθεί άμεσα με πειράματα.
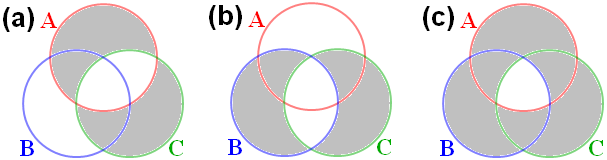
Τί συμβαίνει αν θέσουμε τον πρώτο ανιχνευτή στη ρύθμιση Β, και το δεύτερο ανιχνευτή στη ρύθμιση C, και εξετάζουμε το πόσο συχνά οι δύο ανιχνευτές δίνουν διαφορετικές απαντήσεις; Δηλαδή, πόσο συχνά τα ζεύγη των σωματιδίων εμπίπτουν στη σκιασμένη περιοχή στο σχήμα (b); Και πάλι, η απάντηση είναι 15%.
Πόσο συχνά τα σωματίδια εμπίπτουν στη σκιασμένη περιοχή στο σχήμα (c); Το σχήμα (c) είναι η «ένωση» των δύο συνόλων (a) και (b). Όλα τα σωματίδια τα οποία εμπίπτουν στις σκιασμένες περιοχές στο (a) ή/και στο (b) θα εμπίπτουν επίσης εντός της σκιασμένης περιοχής του (c). Αυτό συνεπάγεται ότι τα σωματίδια θα εμπίπτουν στη σκιασμένη περιοχή του (c) όχι σε περισσότερες από το 30% των περιπτώσεων.
Για να συνοψίσουμε:
(a) Οι ανιχνευτές Α και C δίνουν διαφορετικές απαντήσεις: 15%
(b) Οι ανιχνευτές Β και C δίνουν διαφορετικές απαντήσεις: 15%
(c) Η ένωση του (a) και (b): Το πολύ 30%
Τώρα, τι γίνεται αν θέσουμε τον πρώτο ανιχνευτή στη ρύθμιση Α και το δεύτερο ανιχνευτή στη ρύθμιση Β; Πόσο συχνά οι δύο ανιχνευτές θα δίνουν διαφορετικές απαντήσεις; Αν δίνουν διαφορετικές απαντήσεις, τότε το ζεύγος σωματιδίων πρέπει να πέσει κάπου στη σκιασμένη περιοχή του (c). Ως εκ τούτου, δεν θα μπορούσε αυτό να συμβαίνει σε περισσότερες από 30% μετρήσεις, σωστά; Λάθος! Τόσο η κβαντική θεωρία όσο και το πείραμα, δείχνουν ότι οι απαντήσεις στη ρύθμιση Α και στη ρύθμιση Β είναι διαφορετικές στο 50% των περιπτώσεων. Έχουμε συναντήσει μια μαθηματική αντίφαση!
Αυτό που συνήθως κάνουμε όταν συναντήσουμε μία μαθηματική αντίφαση, είναι ότι γυρνάμε πίσω. Κοιτάζουμε τις υποθέσεις που κάναμε. Μία από τις υποθέσεις μας πρέπει να ήταν εσφαλμένη! Στην αρχή, είπαμε: «Ας υποθέσουμε ότι κάθε σωματίδιο έχει προκαθορισμένες απαντήσεις σε κάθε μία από αυτές τις τρεις ερωτήσεις». Στο πλαίσιο των κύριων ερμηνειών της κβαντομηχανικής, αυτή η υπόθεση είναι λανθασμένη. Τα σωματίδια δεν έχουν προκαθορισμένες απαντήσεις σε κάθε δυνατή μέτρηση. Αντ’ αυτού, θα πρέπει να περιγράψουμε τις καταστάσεις τους με πιθανότητες.
Θα πρέπει επίσης να αναφέρουμε ότι υπάρχουν άλλες ερμηνείες σχετικά με αυτό το συμπέρασμα. Ίσως κάναμε άλλες σιωπηλές υποθέσεις, και ίσως αυτές οι υποθέσεις να είναι οι λανθασμένες. Υπάρχουν πολλές άλλες, οι οποίες έχουν ονόματα όπως «ρεαλισμός», «τοπικότητα», κ.λπ. Αλλά δε θα μπούμε σε αυτά τα ζητήματα προς το παρόν. Θα αφήσουμε απλώς το Θεώρημα του Bell, όπως είναι, μια απόδειξη ότι διαισθητικά, «κάτι πάει στραβά».